2023年3月上旬
2023-03-01 10:01
开始写论文的引言
2023-03-01 11:30
吃饭
2023-03-01 14:42
继续写引言
2023-03-02 10:22
继续写引言
2023-03-06 20:48:06
- 回忆了一下怎么使用我的程序。
mkdir build && cd build && cmake .. make -j32
2023-03-06 22:37:24
- 成功测试发送邮件功能
2023-03-07 00:12:17
- 成功测试计时功能
2023-03-07 10:53:07
- 测试插值算子和延拓算子. 程序为
test/test_ibm_elerian_larangian_interaction.cpp, 测试通过。 考虑到计算效率, 目前固体只使用一阶有限元方法求解。
2023-03-07 16:00:50
- 显式浸没边界法, 程序为
test_ibm_disk_driven_explicit.cpp
使用 ImersedBoundaryMethod 类 set_dolfin_solver
2023-03-07 18:02:31
test_ibm_disk_driven_explicit.cpp 能够运行了, 但是流体的边界条件还不知道怎么设置。
可能需要在CPU中设置, 然后传输到GPU中。
2023-03-08 10:09:21
对于直杆弯曲问题, 固定边界有两种方式: 1. 通过Dirichlet条件限制 2. 通过惩罚项约束
先实现第一种方法的显式时间离散。
现在, test_ibm_bended_bar_explicit_constraint.cpp 能够运行了。
2023-03-08 10:28:36
现在体积力的计算没问题了。
代码位置: 06b5d561eee0c173c3b65442c6d4ef7cfa3d29c3 边界标记: https://github.com/shaoyaoqian/shaoyaoqian.github.io/releases/download/## 20230221/boundaries## 20230308112542.vtu 体积力: https://github.com/shaoyaoqian/shaoyaoqian.github.io/releases/download/## 20230221/forces## 20230308112803.vtu
2023-03-08 14:58:31
弯曲直杆问题的显式计算程序 test_ibm_bended_bar_explicit_constraint.cpp 。
- 测试限制条件。
固体类需要有一个函数, 修改传入的位移或者速度。 GenericSolidSolver 对象几乎是一个无状态的对象, 它不存储当前位置或者初始位置。 真正的数据都存储在 solid_mesh 对象中, 名为_solid_positions , 可以间接通过ImmersedBoundaryMethod获取。
2023-03-08 21:12:57
程序框架的改进
固体求解器不存储以下变量: 1. 固体的当前位置 2. 固体的体积力 固体求解器根据传入的固体的当前位置计算出固体的体积力。但是会存储一些与模型相关的数据,例如: 1. 边界条件存储在boundaries变量中 2. 当前时刻和时间步长 3. 其他与模型相关的变量,例如本构参数,电势等等。
ImmersedBoundaryMethod 中更新 solid solver 位置的函数也不再有用,因此一并删去。
ImmersedBoundaryMethod 增加了限制固体位移的函数。
2023-03-08 21:30:07
写论文的引言
2023-03-09 10:00:34
完成了引言的参考文献
2023-03-09 11:07:06
测试
带约束条件的直杆弯曲算例 test_ibm_bended_bar_explicit_constraint.cpp 的运行结果
参数:
- 固体网格的坐标 (0.45, 0.45, 0.1) (0.55, 0.55, 0.9)
- 网格剖分 {4, 4, 32};
- 流体粘性、密度、时间步长: double nu = 0.01; double rho = 1.0; double dt = 0.0001;
- 背景网格 int3 dim_bg = {65, 65, 65}; double3 dh_bg = {0.0, 0.0, 0.0}; double3 box_size_bg = {1.0, 1.0, 1.0};
计算结果
https://github.com/shaoyaoqian/shaoyaoqian.github.io/releases/download/20230221/bended_bar_020230309111559.vtu
2023-03-09 11:39:40
应变能函数中加入不可压项
kappa = 100000.0
J = det(F)
kappa * (J**2 - 1 - 2*ln(J))2023-03-09 17:05:14
加入了不可压项,时间步长仍为\(0.0001\),仍旧不稳定,这在预料之中。
代码位置
451c31458906e2d2c158fc404c4824418cb3067e ### 结果 
问题
- 边界条件可能没有在计算固体的体积力前施加
- 不可压边界条件不起作用
2023-03-09 20:11:49
问题一:不可压条件
固体的不可压条件可以通过两种方法施加,第一种是拉格朗日乘子法,另一种是通过惩罚项强制\(\text{det}(\mathbb{F})=1\)满足。一般来说,只要选取其中一种即可。浸没边界法中,不可压条件自然存在。整个计算区域的速度场满足无散度条件,相当于使用了拉格朗日乘子法。但是速度经过插值算子传递到固体区域后,无散度边界条件可能不精确满足,因此需要对固体额外施加不可压条件。以后可以看看文章A monolithic projection framework for constrained FSI problems with the immersed boundary method 是怎么施加约束条件的。
问题二:固体位移的Dirichlet边界条件
有两种方法。第一种是每个时间步后将固体强制拉回原位,第二种是惩罚项。目前发现第一种方法不行。张心欣是用的第一种方法,可能是因为它使用的固体本构简单吧,所以他的没问题。IBAMR一直使用的是第二种方法。
2023-03-10 09:25:49
计划
- 符号表
- 完成浸没有限元方法的数学描述
2023-03-10 10:08:57 查看结果
代码位置
168394afa3200c5016eadc8bbfdf21b2b5b2d4cd
参数
int3 dim = {4, 4, 32};
dolfin::Point p2(0.45, 0.45, 0.1);
dolfin::Point p3(0.55, 0.55, 0.9);
double nu = 0.01;
double rho = 1.0;
double dt = 0.00001;
int3 dim_bg = {65, 65, 65};
double3 dh_bg = {0.0, 0.0, 0.0};
double3 box_size_bg = {1.0, 1.0, 1.0};# Constituitive parameters
C = 20000.0 # dyn/cm^2 (2kPa)
bf = 8.0
bt = 2.0
bfs = 4.0
kappa = 1e4 # Penalty for incompressibility
beta = 1e4 # Penalty for boundary conditions
# Boundary markers
bottom = 2
fixed = 1
# Pressure
pressure = 40结果

数据
https://github.com/shaoyaoqian/shaoyaoqian.github.io/releases/download/20230221/position00019920230310101333.vtu
问题
- 惩罚项不够大
- 直杆没有向正上方偏移
2023-03-10 10:23:34 符号表
以下是本论文中使用的符号的非详尽列表。我们将采用粗体字符表示矢量的惯例。
欧拉描述
| Explanation | 中文解释 | |
|---|---|---|
| \(\Omega\) | An open subset of \(\mathbb{R}^n\) | 背景区域 |
| \(\partial \Omega\) | boundary of \(\Omega\) | 区域边界 |
| \(\mathbf{u}\) | Velocity field | 速度场 |
| \(p\) | Pressure field | 压强场 |
| \(\mathbf{n}\) | Unit vector normal to \(\partial \Omega\) | 单位外法向 |
| \(\nabla\cdot\mathbf{u}\) | Divergence of \(\mathbf{u}\) | 速度散度 |
| \(\nabla\mathbf{u}\) | Gradient of \(\mathbf{u}\) | 速度梯度 |
| \(\Delta\mathbf{u}\) | Laplacian of u, defined by \(\Delta=\nabla\cdot\nabla\) | 拉普拉斯算子 |
| \(\langle\cdot,\cdot\rangle\) | \(L^2\)-inner product on \(\Omega\) | \(L^2\)内积 |
| \(\|\cdot\|_k\) | Norm defined by the \(H^k\)-inner product on \(\Omega\) if \(k = 0, 1\) | \(H^{k}\)范数 |
| \(\|\cdot\|_2\) | Euclidian norm | 欧几里得范数 |
| \(\mathbf{x}\) | \(\mathbf{x}=(x_1,x_2,x_3)\) Eulerian coordinates | 欧拉坐标 |
拉格朗日描述
参数
| Explanation | 中文解释 | |
|---|---|---|
| \(\mu\) | (Dynamic) Viscosity | 动力粘性 |
| \(\rho\) | Density | 密度 |
| \(\nu\) | Kinematic viscosity, defined as nu:=mu//rho | 运动粘性 |
| \(\Delta t\) | Timestep | 时间步长 |
| \(Re\) | Reynolds number | 雷诺数 |
| \(h\) | Discretization parameter1 | 空间离散参数 |
矩阵的性质
| Explanation | 中文解释 | |
|---|---|---|
| \(L^2(\Omega)\) | Space of square-integrable functions on \(\Omega\) | \(\Omega\)上的平方可积函数 |
| \(H^k(\Omega)\) | Space of \(L^2\)-functions on \(\Omega\) with derivatives up to order \(k\) which are also in \(L^2(\Omega)\) | \(H^{k}\)空间 |
| \(H_0^k(\Omega)\) | Space of functions in \(H^k(\Omega)\) which equal zero on \(\partial \Omega\) | \(H^1\)空间 |
| \(H^{-1}\) | Dual space of \(H^1\) | \(H^1\)的对偶空间 |
固体力学
| Explanation | 中文解释 | |
|---|---|---|
| \(\boldsymbol \sigma\) | The Cauchy stress tensor | 柯西应力张量 |
| \(\mathbb{P}\) | the first Piola–Kirchhoff stress tensor | 第一PK应力张量 |
| \(W\) | Strain energy density function | 应变能密度函数 |
| \(E\) | Elastic potential energy function | 弹性势能函数 |
| \(?\) | Kinetic energy function | 动能函数 |
| \(B\) | A region in three-dimensional Euclidean point space(\(\mathbb{R}^n\)), called configuration of \(\mathcal{B}\) | 固体的构型 |
| \(B_r\) | A specific configuration of \(\mathcal{B}\) | 参考构型 |
| \(B_t\) | Current configutation of \(\mathcal{B}\) | 现时构型,当前构型 |
| \(\mathcal{B}\) | A body, considered as a set of elements, or particles, or material points, whatever | 固体 |
| \(\mathcal{X}(\mathbf{X},t)\) | bijection mapping between \(B_r\) and \(B_t\) | |
|---|---|---|
| \(\mathbf{X}\) | \(\mathbf{X}=(X_1,X_2,X_3)\)Coordinates of material points at reference configuration | 固体粒子在参考构型的坐标 |
| t | current time | 当前时间 |
| \(T\) | total time interval | 时间间隔 |
浸没边界法
| \(\mathcal{S}(\mathbf{X},t)\) | prolongation operation, distribution operator | 延拓算子 |
| \(\mathcal{J}(\mathbf{\mathbf{X}},t)\) | restriction operator, interpolation operator | 插值算子 |
2023-03-10 16:40:37 完成文章的第二章
图1描述了一物体\(\mathcal{B}\)在固定的背景区域\(\Omega\)中运动的过程。 物体 \(\mathcal{B}\) 所有质点空间坐标的集合称为其构型,记为\(B\)。\(t\in[0,T]\) 表示时间,\(B_t\) 表示固体 \(\mathcal{B}\) 在 \(t\) 时刻的构型,称为现时构型。对任意时间\(t\),有唯一的构型\(B_t\)与之对应,这些构型的集合\(\{B_t\}\)称为物体\(\mathcal{B}\)在时间\([0,T]\)的运动。\(\mathcal{B}_r\)表示固体在\(t=0\)时刻的构型,称为参考构型。\(\mathbf{X}\)表示物体\(\mathcal{B}\)任一质点在参考构型中的空间坐标,\(\mathbf{X}=\) \(\left(X_{1}, X_{2}, \ldots\right)\in B_{r} \subset \mathbb{R}^{d}, d=2,3\) ,称之为拉格朗日坐标。\(\mathcal{X}(\mathbf{X},t)\)是从\(B_r\)到\(B_t\)的映射,映射\(\mathcal{X}(\mathbf{X},t)\)称为固体从\(\mathcal{B}_r\)到\(\mathcal{B}_t\)的形变。\(\mathcal{X}(\mathbf{X},t)\) 是定义在参考构型 \(B_r\) 上的物理量,以\(\mathbf{X}\)为自变量,我们称之为拉格朗日描述。区域\(\Omega\)表示流固耦合系统占据的物理区域,\(\Omega/B_t\)为流体区域,我们讨论定义在\(\Omega\)上的方程,不对流体区域进行单独描述。\(\mathbf{x}\)表示\(\Omega\)中的任意一点,\(\mathbf{x}=\left(x_{1}, x_{2} \ldots\right)\in \Omega \subset \mathbb{R}^{d}, d=2,3\),称之为欧拉坐标。\(\mathbf{u}(\mathbf{x},t)\)、\(p(\mathbf{x},t)\)分别表示流固耦合系统的速度场和压力场。
Figure 1 describes the motion of an body \(\mathcal{B}\) in a fixed background domain \(\Omega\). The set of spatial coordinates of all particles of body \(\mathcal{B}\) is called its configuration, denoted by \(B\). \(t\in[0,T]\) represents time, \(B_t\) represents the configuration of body \(\mathcal{B}\) at time \(t\), which is called the current configuration. For any time \(t\), there is a unique configuration \(B_t\) corresponding to it. The set of these configurations \({B_t}\) is called the motion of body \(\mathcal{B}\) during time \([0,T]\). \(B_r\) denotes the configuration of the body at \(t=0\), called the reference configuration. \(\mathbf{X}\) represents the spatial coordinate of a specific particle in the reference configuration of body \(\mathcal{B}\), \(\mathbf{X}=\left(X_{1}, X_{2}, X_{3}\right)\in B_{r} \subset \mathbb{R}^{e}\), which is called the Lagrangian coordinate. \(\mathcal{X}(\mathbf{X},t)\) is the mapping from \(B_r\) to \(B_t\), which is called the deformation of the body from \(B_r\) to \(B_t\). \(\mathcal{X}(\mathbf{X},t)\) is a physical quantity defined on the reference configuration \(B_r\). We call it the Lagrangian description, with \(\mathbf{X}\) as its independent variable. The domain \(\Omega\) represents the physical domain occupied by the fluid-solid coupling system. \(\Omega/B_t\) denotes the fluid domain. We discuss equations defined on \(\Omega\) and do not separately describe the fluid domain. \(\mathbf{x}\) represents any point in \(\Omega\), \(\mathbf{x}=\left(x_{1}, x_{2}, x_{3}\right)\in \Omega \subset \mathbb{R}^{3}\), which is called the Eulerian coordinate.
假设固体和流体均不可压且密度相等,流体为牛顿流体,固体为粘超弹性固体,流固耦合系统的柯西应力张量为
Assuming that both the solid and fluid are incompressible and have equal densities, the fluid is assumed to be a Newtonian fluid and the solid is assumed to be a viscous hyperelastic material, then the Cauchy stress tensor of the fluid-structure coupling system is given by \[ \boldsymbol{\sigma}(\mathbf{x}, t)=\boldsymbol{\sigma}^{\mathrm{f}}(\mathbf{x}, t)+ \begin{cases}\boldsymbol{\sigma}^{\mathrm{e}}(\mathbf{x}, t) & \mathbf{x} \in B_t \\ \mathbf{0} & \mathbf{x}\in\Omega/B_t\end{cases} \] Here are the meanings of the quantities and variables that appear in the above equations in details. \[ \boldsymbol{\sigma}^{\mathrm{f}}(\mathbf{x}, t)=-p(\mathbf{x}, t) \mathbb{I}+\mu\left[\nabla \mathbf{u}(\mathbf{x}, t)+(\nabla \mathbf{u}(\mathbf{x}, t))^{\mathrm{T}}\right] \]
\[ \boldsymbol{\sigma}^{\mathrm{e}}(\mathbf{x}, t)=\boldsymbol{\sigma}^{\mathrm{e}}(\boldsymbol{\mathcal{X}}(\mathbf{X}, t), t) = J^{-1}(\mathbf{X}, t)\mathbb{P}^{\mathrm{e}}(\mathbf{X}, t)\mathbb{F}^{\mathrm{T}}(\mathbf{X}, t) \]
\(\mathbb{I}\)为单位张量,\(\mu\)为运动粘性,\(\mathbb{F}(\mathbf{X},t)\)为形变梯度,\(J(\mathbf{X}, t)=\operatorname{det}(\mathbb{F}(\mathbf{X}, t))\),\(\mathbb{P}(\mathbf{X},t)\)为第一Piola-Kirchhoff应力张量,可以通过对应变能函数\(W(\mathbb{F})\)求导得到
\(\boldsymbol{\sigma}^{\mathrm{f}}(\mathbf{x}, t)\) is the fluid-like component of stress tensor which exits everywehre in \(\Omega\), \(\mathbf{u}(\mathbf{x},t)\) and \(p(\mathbf{x},t)\) represent the velocity field and pressure field of the fluid-solid coupling system, respectively. \(\mathbb{I}\) is the identity tensor, \(\mu\) is the dynamic viscosity. \(\boldsymbol{\sigma}^{\mathrm{f}}(\mathbf{x}, t)\) is the elastic component of stress tensor which only exists in solid domain. \(\mathbb{F}(\mathbf{X},t)\) is the deformation gradient, \(J(\mathbf{X}, t)=\operatorname{det}(\mathbb{F}(\mathbf{X}, t))\), and \(\mathbb{P}(\mathbf{X},t)\) is the first Piola-Kirchhoff stress tensor, which can be obtained by taking the derivative of the corresponding strain energy function \(W(\mathbb{F})\) \[ \mathbb{P}^{\mathrm{e}}=\frac{\partial W^{\mathrm{e}}}{\partial \mathbb{F}} \] 浸没边界法的控制方程可以通过动量守恒定律和质量守恒定律推导。在求解中,\(\boldsymbol{\sigma}^f(\mathbf{x}, t)\)需采用欧拉描述,\(\boldsymbol{\sigma}^{e}(\mathbf{x}, t)\)需采用拉格朗日描述,它们之间通过与delta核函数的积分变换建立起联系。本文采用了Boyce等人推导的方程组。
The governing equations of the Immersed Boundary Method can be derived from the principles of conservation of momentum and mass. When we solve the problem practically, the fluid stress tensor \(\boldsymbol{\sigma}^f(\mathbf{x}, t)\) is expressed in Eulerian description, while the solid stress tensor \(\boldsymbol{\sigma}^{e}(\mathbf{x}, t)\) is expressed in Lagrangian description. The relationship between them is established through integration with the delta kernel function. Equations derived by Boyce et al. is adopted in this paper. \[ \rho(\frac{\partial \bf{u}}{\partial t}+(\bf{u}\cdot \nabla)\bf{u}) +\nabla p -\mu \Delta \bf{u} = \bf{f} \] \[ \nabla\cdot \bf{u} = 0 \] \[ \int_{\bf{B}_{r}}\bf{F}\cdot \bf{V}d\bf{X} =-\int_{\bf{B}_{r}}\mathbb{P} :\nabla \bf{V}d\bf{X} \] \[ \bf{f}(x,t) = \int_{\bf{B}_{r}} \bf{F}(\bf{X},t)\delta(x-\chi(\bf{X},t)d\bf{X} \] \[ \frac{\partial{\chi (\bf{X,t})}}{\partial t} =\int_{\Omega}\bf{u}(x,t)\delta (\chi (\bf{X},t)-x)dx \]
2023-03-11 01:26:50 多孔介质固体的流固耦合
灌注压力的求解
- \(M_b\):常数
- \(p\):是灌注压力,和流体的压力无关
- \(f(J)=\frac{2(J(\mathbf{X}, t)-1-\ln (J(\mathbf{X}, t)))}{(J(\mathbf{X}, t)-1)^2}\)
- \(E(M,J)\):一个标量,与\(m^n\)和\(J^n\)
\[ \frac{P^{n+\frac{1}{2}}-P^n}{\triangle t / 2}-M_b f\left(J^n\right) \nabla_{\mathbf{X}} \cdot\left(J^n \mathbb{F}^{-1} \mathbf{K} \mathbb{F}^{-T} \nabla P^{n+\frac{1}{2}}\right)=E\left(M^n, J^n\right) \]
在求解此方程之前,我们先考虑带矩阵系数的泊松方程。
带矩阵系数的泊松方程
带矩阵系数的泊松方程为: \[ -\nabla \cdot(\boldsymbol{A}\nabla u) = f \] 其中,\(u\)是未知函数,\(f\)是已知函数,\(\boldsymbol{A}\)是一个矩阵。其变分形式可以表示为:找到一个函数\(u \in H^1(\Omega)\),满足下列变分问题:
\[ \int_{\Omega} \boldsymbol{A}\nabla u \cdot \nabla v \;dx = \int_{\partial \Omega} A\nabla u\cdot \mathbf{n} v \;ds+\int_{\Omega} fv \;dx \quad\forall \;v \in H^1(\Omega) \]
其中\(\Omega\)是定义域,\(\partial \Omega\)是\(\Omega\)的边界。若\(g=A\nabla u\cdot \mathbf{n}\)为已知函数,则能求解。
2023-03-11 12:21:22
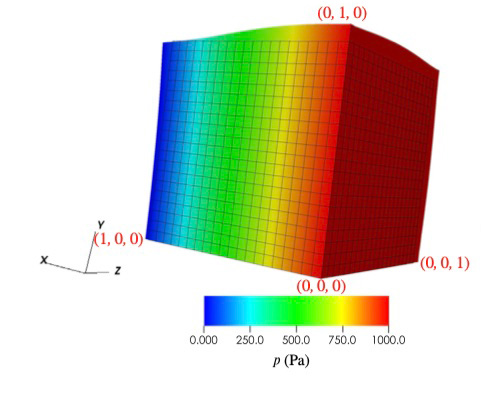
算例1:立方体膨胀 swelling for a cube
背景区域:区域为 \(1 \times 1 \times 1 \mathrm{~cm}^3\) ,网格剖分为 \(96 \times 96 \times 96\) 。
质疑:背景区域和固体区域一样大么?
固体的位移边界条件:\(x=0,y=0,z=0\)三个平面的法向位移为零。
源项:\(S=0\)。
灌注压力:
- \(x=0\)平面施加与时间相关的压力,\(p_{\mathrm{bc}}=10^3\left(1-\exp \left(-t^2 / 0.25\right)\right)\)。
- \(x=1\)平面的压力恒为零。
- 其他平面为零Neumann边界条件。
预期结果:
由于平面\(x=0\)施加了空隙压力(pore pressure),立方体会像海绵一样膨胀。
2023-03-11 12:21:44
代码位置
168394afa3200c5016eadc8bbfdf21b2b5b2d4cd
参数
int3 dim = {4, 4, 32};
dolfin::Point p2(0.45, 0.45, 0.1);
dolfin::Point p3(0.55, 0.55, 0.9);
double nu = 0.01;
double rho = 1.0;
double dt = 0.000005;
int3 dim_bg = {65, 65, 65};
double3 dh_bg = {0.0, 0.0, 0.0};
double3 box_size_bg = {1.0, 1.0, 1.0};# Constituitive parameters
C = 20000.0 # dyn/cm^2 (2kPa)
bf = 8.0
bt = 2.0
bfs = 4.0
kappa = 1e1 # Penalty for incompressibility
beta = 1e7 # Penalty for boundary conditions
# Boundary markers
bottom = 2
fixed = 1
# Pressure
pressure = 40结果

数据
https://github.com/shaoyaoqian/shaoyaoqian.github.io/releases/download/20230221/position00017020230311122948.vtu
问题
- 直杆没有向正上方偏移
- 参数kappa过大是否会导致直杆不会弯曲



